Globally Optimal Linear Model Fitting with Unit-Norm Constraint

Yinlong Liu*, Yiru Wang*, Manning Wang, Guang Chen^†, Alois Knoll, Zhijian Song^†

International Journal of Computer Vision (2022, IF=7.410)

Abstract

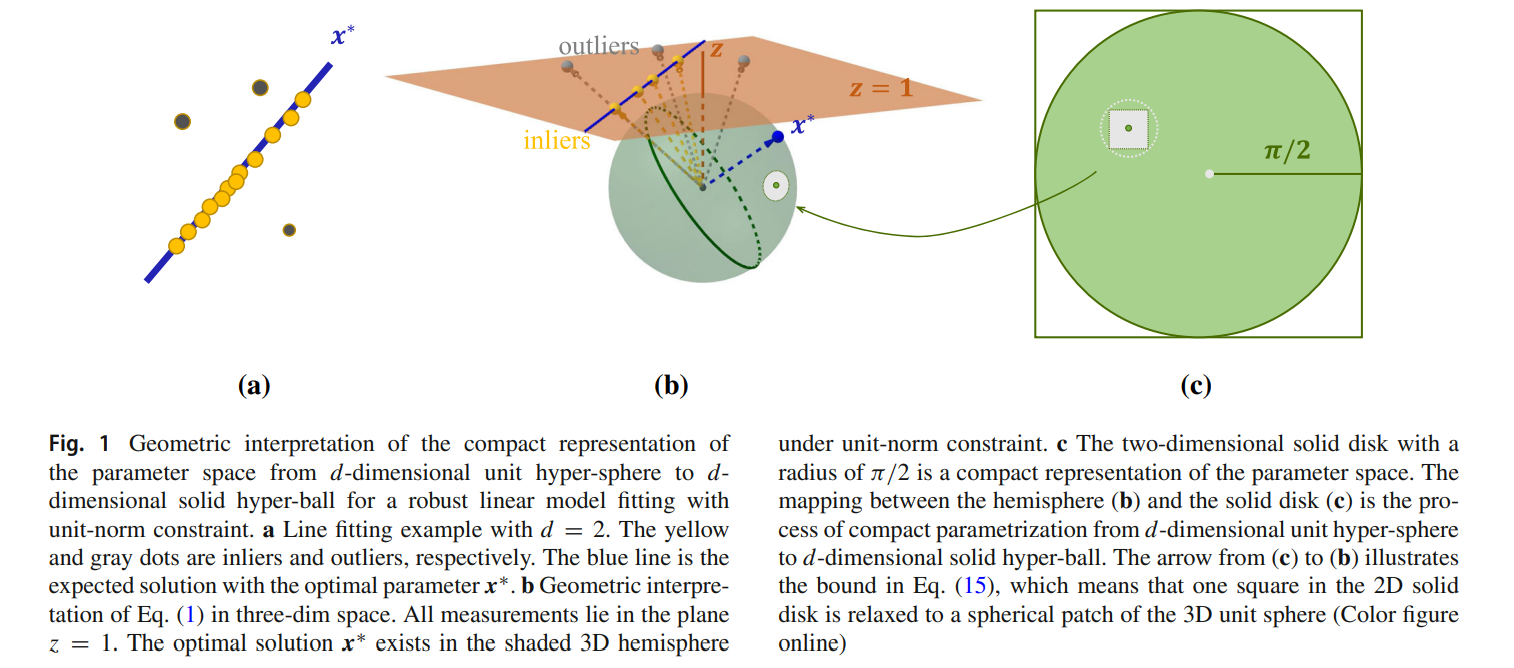
Robustly fitting a linear model from outlier-contaminated data is an important and basic task in many scientific fields, and it is often tackled by consensus set maximization. There have been several studies on globally optimal methods for consensus set maximization, but most of them are currently confined to problems with small number of input observations and low outlier ratios. In this paper, we develop a globally optimal algorithm aiming at consensus set maximization to solve the robust linear model fitting problems with the unit-norm constraint, which is based on the branch-and-bound optimization framework. The unit-norm constraint is utilized to fix the unknown scale of linear model parameters, and we propose a compact representation of the unit-bounded searching domain to avoid introducing the additional non-linearity in the unit-norm constraint. The compact representation leads to a geometrically derived bound, which accelerates the calculation and enables the method to handle the problems with large number of observations. Experiments on both synthetic and real data show that the proposed algorithm outperforms existing globally optimal methods, especially in low dimensional problems with large number of input observations and high outlier ratios.

Paper Link: https://link.springer.com/article/10.1007/s11263-022-01574-z

Code Link: https://github.com/YiruWangYuri/Demo-for-GoCR